I’m working on a project that’ll require the use of a non-contact detection system. A few technologies achieve this, such as Sonar, capacitive sensing, inductive sensing, and optical detection. Sonar and optical won’t work due to the enclosure, and capacitive sensing has the disadvantage of being susceptible to temperature and humidity, leaving me to take a crack at inductive sensing. This post is my attempt to explain the principles behind induction sensing, all data and designs can be found in the project repositroy.
Bit of Background
The basic principle behind inductive sensing lies in the Self Resonating Frequency (SRF) of the planar coil inductor (PCI). In practice, the coil won’t be a perfect inductor; parasitic capacitive and trace resistance is an unavoidable reality. Calculating the SRF is pretty straight forward.
$$ SRF = \frac{1}{2\pi C L} $$
Where C is the total capacitance, and L is the total inductance. From this, you can see that SRF can be shifted by tweaking individual parameters.
When current is applied to a wire or trace in this case, it’ll induce a magnetic field around that trace. If these traces are arranged in a loop/coil, the magnetic fields will be concentrated into the center.
When this magnetic field is brought into close proximity of a conduction object, like a copper sheet, it’ll induce circular currents in the material known as Eddy currents. In the same way, the current passing through a wire generates a magnetic field, these Eddy currents create their own magnetic field that opposes the origin field; this is known as Lenz Law. This opposing field effectively reduces the inductance, shifting the SRF. This shift is what indicates the somthing conductive is near the PCI.
Inductance has two components, self-inductance and mutual inductance, which I’ll discuss below.
Mutual Inductance
I’m going to try and explain this without going too deep. As per Lens Law, when the magnetic flux from one loop (A) flows through a second loop (B), a constant parameter proportional to the amount of magnetic flux $\Phi_B$ through loop B, divided by the current $I_A$ in loop A is known as the mutual inductance $M_{BA}$. This principle also works in reverse, making $M_{BA} = M_{AB}$
$$ M_{BA} = \Phi_B /I_A $$
This mutual inductance is defined by the Newman formula [1].
$$ M_{ij} = \frac{\mu_0R_iR_i}{2} \int_{\theta=0}^{2\pi} \frac{cos\theta}{\sqrt{R_i^2+R_j^2+d^2-2R_iR_jcos\theta}}d\theta $$
Where:
- $ R_i, R_j $: Average radius of $i^{th}$ and $j^{th}$ loop between coil x and y, respectively
- $ d $: Distance between coils
I found this method to be quite computationally heavy. A 4 layer board with 15 turns per layer requires 2700 computation iterations. Furthermore, each iteration requires the function to be integrated from 0 to 2$\pi$. Instead, I’ll use a more straightforward approximation method, which calculates a constant coupling coefficient between two inductors.
$$ M_{12} = K\sqrt{L_1L_2} $$
The K approximation is defined by the following paper [2]
$$ K = \frac{N^2}{0.64[(0.184x^3 - 0.525x^2 + 1.038x + 1.001)(1.67N^2 - 5.84N + 65)]} $$
Where
- x: Distance between layers in mm
- N: Number of turns in the layer
Self Inductance
Because the inductor is made up of consecutive loops, the self-inductance can be explained much like the mutual inductance. The induced magnetic flux from the first loop will pass through the subsequent loops of the inductor. According to Faradays Law, this flux will induce a current that opposes the incoming current. When this coil is flattened into two dimensions, its self-inductance can be approximated with the equation below [3]
$$ L = \frac{\mu_0N^2D_{avg}C_1}{2}(ln(\frac{C_2}{\sigma})+C_3\sigma+C_4\sigma^2) $$
$$ \sigma = \frac{D_{outer} - D_{inner}}{D_{outer} + D_{inner}} $$
Where:
- $ \mu_0 $: Free space permeability
- $ N $: Number of turns
- $ D_{avg} $: Average diameter of coil
- $ \sigma $ Fill Factor
- $ C_1, C_2, C_3, C_4 $: Geometric coefficents [3]
Series Configuration
Applying Kirchhoff’s Voltage Law to a string of Inductors in series, with the addition of the mutual inductance, yields a simple summing equation similar to a network of resistors in series. If the inductors are wound so that induced magnetic fields are in the same direction, the mutual inductances will be additive.
$$ L_{eff} = L_a + M_{ab} + L_b + M_{ba} $$
The total Effective Inductance $ L_{eff} $ is the sum of the series Self Inductance $ L_a, L_b $ and the Mutual Inductances $ M_a, M_b $
Parallel Configuration
In the parallel case, I find it easier to use a system of equations to define the two branch voltages.
$$ V_a = L_a\frac{di_a}{dt} + M_{ab}\frac{di_b}{dt} $$ $$ V_b = L_b\frac{di_b}{dt} + M_{ba}\frac{di_a}{dt} $$
The Node Voltages $ V_a, V_b $ are the sum of voltages across Inductors $ L_a, L_b $: and the Mutual Inductance $ M_ab, M_ba $. Using the knowledge that $V_a$ and $V_b$ are equal, and assuming the inductors are identical, we can combine and reduce the equations above to calculate the effective inductance
$$ L_{p_eff} = \frac{L_aL_b-M^2}{L_a+L_b-2M}$$
The goal of connecting the inductors in a parallel configuration isn’t to gain an increase in inductance. Instead, the PCI resistance should be dramatically decreased compared to a coil with similar physical dimensions, resulting in a more efficient drive circuit.
Planar Coil Inductor Layout
As mentioned above, the total inductance will be made up of two parts, self-inductance and mutual inductance. To ensure the coils are correctly coupled, the coiling direction needs to switch directions on each subsequent layer.
Trace Resistance
The Trace resistance is reasonably straight forward. The trace length per layer is the arch length of the spiral, as the radius increase as a function of the angle.
$$ l = \int\limits_{0}^{2n\pi}{(r_0+r_{\Delta})d\theta} $$
Where:
- $ l $: Trace length
- $ n $: Number of turns
- $ r_0 $: Inner Radius
- $ r_{\Delta} $: Trace width
Finally, the trace resistance can be calculated.
$$ R_{DC} = \rho\frac{L}{T*W} $$
Where:
- $ \rho $: Resistivity (copper = 17.1E-6 [$\Omega$-mm/mm]
- $ l $: Length [mm]
- $ T $: Thickness (1oz copper 0.018-0.035mm)
- $ W $: Width
Circuit Capacitance
Because the inductors resonant frequency is dependant on both the inductance and capacitance, a small fluctuation in an already small parasitic capacitance can result in a significant resonate frequency shift. Therefore, a sensor capacitor much greater than the unknown parasitic capacitance needs to be selected to minimize significant inductance changes.
Assume the parasitic capacitance is 1pF with a parallel sensor capacitor of 10pF, the inductors’ nominal value is 10uH. If the parasitic capacitance were to fluctuate by 50%, the effective inductance would shift by about 5%. However, If a sensor capacitor of 1nF was used, a 50% change in parasitic capacitance would result in less than 100th of a percent change in the effective inductance.
| Sensor C [F] | Parastic C [F] | Nominal L [H] | Resonante F [Hz] | Equivalent L [H] | Percent Change [%] |
|---|---|---|---|---|---|
| 10.000E-12 | 1.000E-12 | 10.000E-06 | 15.175E+06 | 10.000E-06 | 0.000 |
| 10.000E-12 | 1.100E-12 | 10.000E-06 | 15.106E+06 | 10.091E-06 | 0.909 |
| 10.000E-12 | 1.500E-12 | 10.000E-06 | 14.841E+06 | 10.455E-06 | 4.545 |
| 10.000E-12 | 900.000E-15 | 10.000E-06 | 15.244E+06 | 9.909E-06 | -0.909 |
| 10.000E-12 | 500.000E-15 | 10.000E-06 | 15.532E+06 | 9.545E-06 | -4.545 |
| 1.000E-09 | 1.000E-12 | 10.000E-06 | 1.591E+06 | 10.000E-06 | 0.000 |
| 1.000E-09 | 1.100E-12 | 10.000E-06 | 1.591E+06 | 10.001E-06 | 0.010 |
| 1.000E-09 | 1.500E-12 | 10.000E-06 | 1.590E+06 | 10.005E-06 | 0.050 |
| 1.000E-09 | 900.000E-15 | 10.000E-06 | 1.591E+06 | 9.999E-06 | -0.010 |
| 1.000E-09 | 500.000E-15 | 10.000E-06 | 1.591E+06 | 9.995E-06 | -0.050 |
On the other hand, you can’t just throw in 1uF capacitor in and be on your way. The more capacitance you add to the systems, the more high-frequency energy gets shunted away, lowering the bandwidth. In the figure below, at 1nF, the gain at the resonate frequency is around -1.7dB. This means that for every volt put into the system, 822mV comes out, which is very measurable.

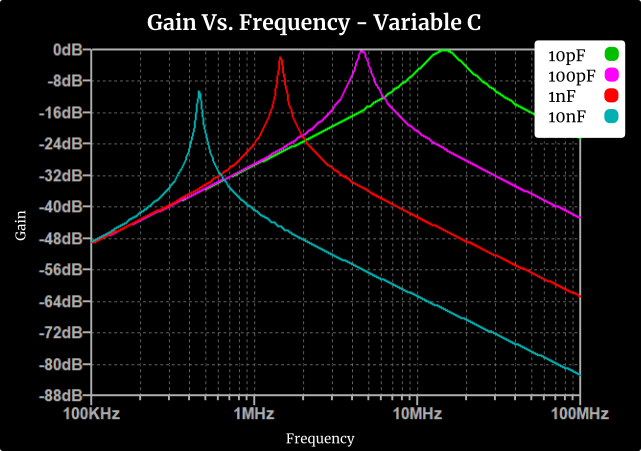
To better approximate the system, I will try to approximate the parasitic capacitance. Using the knowledge that there’s a voltage gradient through the PCI, with the source voltage at the input and ground at the output, I’m choosing to approximate the parasitic capacitance as two long parallel plates spiralled around in a coil.
$$ C = \frac{\epsilon * w * l}{d}$$
Where
- $\epsilon$ is the relative electric permeability of the FR4 material (~4.4)
- w is the trace width
- l is the trace length per layer
- d is the thickness of the FR4 material
Validation
To make sure my math is on the right track, I’m using the Texas Instruments online coil designer tool[5]. Unfortunately, this tool can’t approximate the inductor value of a PCI wired in parallel. Below I’ve listed some comparison results for the calculated Inductor value, parasitic capacitance, Resonate frequency and trace resistance. This is only a small subset of the data; the complete database can be in the here
The coils ID is a description of its physical dimensions.
Inductor approximation
| Coil Name | Self L Approximation | Total L Approximation | TI Self L | TI Total L | Total L Error |
|---|---|---|---|---|---|
| C106102200s | 1.349E-06 | 4.069E-06 | 1.110E-06 | 3.350E-06 | 719.2E-09 |
| C106152200s | 3.167E-06 | 9.898E-06 | 2.696E-06 | 8.423E-06 | 1.5E-06 |
| C106202200s | 6.001E-06 | 18.882E-06 | 5.228E-06 | 16.441E-06 | 2.4E-06 |
| C106102400s | 2.346E-06 | 7.080E-06 | 2.060E-06 | 6.213E-06 | 867.1E-09 |
| C106152400s | 5.201E-06 | 16.256E-06 | 4.641E-06 | 14.498E-06 | 1.8E-06 |
| C106202400s | 9.382E-06 | 29.523E-06 | 8.475E-06 | 26.622E-06 | 2.9E-06 |
| C106104200s | 1.349E-06 | 15.831E-06 | 1.112E-06 | 12.420E-06 | 3.4E-06 |
| C106154200s | 3.167E-06 | 39.774E-06 | 2.690E-06 | 32.116E-06 | 7.7E-06 |
| C106204200s | 6.001E-06 | 76.336E-06 | 5.220E-06 | 63.131E-06 | 13.2E-06 |
| C106104400s | 2.346E-06 | 27.544E-06 | 2.060E-06 | 23.004E-06 | 4.5E-06 |
| C106154400s | 5.201E-06 | 65.325E-06 | 4.641E-06 | 55.354E-06 | 10.0E-06 |
| C106204400s | 9.382E-06 | 119.354E-06 | 8.475E-06 | 102.338E-06 | 17.0E-06 |
Parasitic Capacitance
TI’s coil designer doesn’t explicitly give the parasitic capacitance. Instead, the Self Resonant Frequency is provided, and total inductance is given. With these two values, the parasitic capacitance can be calculated. Sadly, I don’t have any reference for how they got their numbers, so I will stick with my capacitance approximation and modify it if needed.
| Coil Name | Approximated Parasitic C | TI SRF | Calculated Parasitic C | Difference |
|---|---|---|---|---|
| C106102200s | 2.9487E-12 | 40.360E+06 | 4.642E-12 | 36.48% |
| C106152200s | 5.2616E-12 | 22.399E+06 | 5.994E-12 | 12.22% |
| C106202200s | 8.1335E-12 | 14.479E+06 | 7.349E-12 | 10.67% |
| C106102400s | 4.3462E-12 | 25.372E+06 | 6.333E-12 | 31.37% |
| C106152400s | 7.3579E-12 | 15.075E+06 | 7.688E-12 | 4.30% |
| C106202400s | 10.9285E-12 | 10.260E+06 | 9.039E-12 | 20.91% |
| C106104200s | 2.4683E-12 | 20.996E+06 | 4.626E-12 | 46.65% |
| C106154200s | 4.4043E-12 | 11.470E+06 | 5.995E-12 | 26.53% |
| C106204200s | 6.8082E-12 | 7.389E+06 | 7.349E-12 | 7.36% |
| C106104400s | 3.6381E-12 | 13.186E+06 | 6.333E-12 | 42.55% |
| C106154400s | 6.1590E-12 | 7.715E+06 | 7.688E-12 | 19.89% |
| C106204400s | 9.1478E-12 | 5.232E+06 | 9.042E-12 | 1.17% |
Trace Resitance
There are two purposes for measuring trace resistance. As mentioned above, the coil’s resistance will affect the power dissipated by the coil. But additionally, it’s a manufacturing check. If the measured resistance differs too much from the expected value, it would indicate there may be a PCB defect like a short.
| Coil Name | Calculated Trace Resistance | TI Trace Resistance | Difference |
|---|---|---|---|
| C106102200s | 0.981 | 1.200 | 0.219 |
| C106152200s | 1.472 | 2.619 | 1.147 |
| C106202200s | 1.962 | 3.389 | 1.427 |
| C106102400s | 1.598 | 1.818 | 0.220 |
| C106152400s | 2.397 | 3.100 | 0.703 |
| C106202400s | 3.196 | 4.630 | 1.434 |
| C106104200s | 2.894 | 2.396 | 0.498 |
| C106154200s | 4.340 | 4.340 | 0.000 |
| C106204200s | 5.787 | 6.778 | 0.991 |
| C106104400s | 4.712 | 3.636 | 1.076 |
| C106154400s | 7.068 | 6.199 | 0.869 |
| C106204400s | 9.424 | 9.260 | 0.164 |
Resonate Frequency
Finally, with the effective inductance, parasitic capacitance, and sensor capacitance, the circuit’s resonate frequency can be calculated.
| Coil Name | Calculated Resonate Frequency | TI Resonate Frequency | Error |
|---|---|---|---|
| C106102200s | 2.472E+06 | 2.743E+06 | 9.89% |
| C106152200s | 1.581E+06 | 1.729E+06 | 8.54% |
| C106202200s | 1.142E+06 | 1.236E+06 | 7.63% |
| C106102400s | 1.871E+06 | 2.012E+06 | 6.99% |
| C106152400s | 1.231E+06 | 1.316E+06 | 6.43% |
| C106202400s | 910.547E+03 | 970.507E+03 | 6.18% |
| C106104200s | 1.254E+06 | 1.424E+06 | 11.96% |
| C106154200s | 789.467E+03 | 885.439E+03 | 10.84% |
| C106204200s | 568.526E+03 | 631.114E+03 | 9.92% |
| C106104400s | 949.397E+03 | 1.046E+06 | 9.24% |
| C106154400s | 614.966E+03 | 673.882E+03 | 8.74% |
| C106204400s | 453.639E+03 | 495.275E+03 | 8.41% |
Testing
I’m looking to test how closely my SRF and trace resistance approximation lines up with reality with this setup.
SRF Testing
To determine the SRF of the PCI, I’ll be measuring the voltage gain at varying frequencies using a function generator and oscilloscope. To better locate the resonate frequency, a damping resistor is added in series with the PCI to dissipate a more significant amount of energy around the resonate frequency.

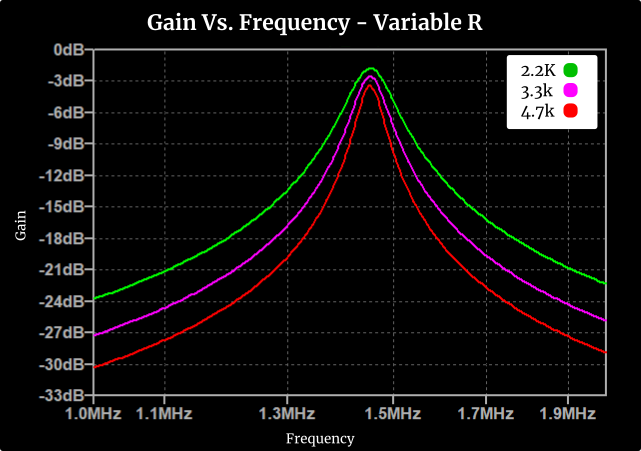
Note: After painstakingly measure the gain of all 36 PCI over many frequencies, almost 1000 measurements, I later remembered I could measure the SRF by applying a square wave to the input and measure the resulting damped oscillations… live and learn
Trace Resistance
Measuring the trace resistance with my current setup will be a bit of a challenge. The resistance of the traces is relatively low. Therefore a standard 2 wire measurement won’t work. Instead, because I don’t have my own 4-wire measurement setup, I’ll need to hack together my own. This can be done by connecting an amp meter in series with a DC power supply, energizing the coil, then measure the voltage across the coil, good ole fashion Ohms Law.
Results
Now for the moment, I’ve been looking for sweet, sweet verification…

Sensor Resonate Frequency Results
As mentioned earlier in the post, the resonate frequency is a function of the inductance and total capacitance. Because of this, there’s technically an infinite number of combinations of L and C that could equal the resonate frequency. Therefore, with the current test setup I have, a comparison of this frequency should be enough to indicate that my approximation is on the right track.
| Coil Name | Resonate Frequency Approximation | TI Resonate Frequency | Measured Resonate Frequency | Error Percentage [Approx, TI] |
|---|---|---|---|---|
| C106102200s | 2.472E+06 | 2.743E+06 | 2.504E+06 | 1.27% 9.57% |
| C106152200s | 1.581E+06 | 1.729E+06 | 1.585E+06 | 0.26% 9.06% |
| C106202200s | 1.142E+06 | 1.236E+06 | 1.127E+06 | 1.26% 9.63% |
| C106102400s | 1.871E+06 | 2.012E+06 | 1.845E+06 | 1.44% 9.07% |
| C106152400s | 1.231E+06 | 1.316E+06 | 1.220E+06 | 0.95% 7.90% |
| C106202400s | 910.547E+03 | 970.507E+03 | 886.300E+03 | 2.74% 9.50% |
| C106104200s | 1.254E+06 | 1.424E+06 | 1.245E+06 | 0.69% 14.36% |
| C106154200s | 789.467E+03 | 885.439E+03 | 787.500E+03 | 0.25% 12.44% |
| C106204200s | 568.526E+03 | 631.114E+03 | 558.800E+03 | 1.74% 12.94% |
| C106104400s | 949.397E+03 | 1.046E+06 | 922.300E+03 | 2.94% 13.41% |
| C106154400s | 614.966E+03 | 673.882E+03 | 604.200E+03 | 1.78% 11.53% |
| C106204400s | 453.639E+03 | 495.275E+03 | 438.000E+03 | 3.57% 13.08% |
| C106104200p | 2.508E+06 | 2.489E+06 | 0.74% | |
| C106154200p | 1.579E+06 | 1.561E+06 | 1.18% | |
| C106204200p | 1.137E+06 | 1.095E+06 | 3.85% | |
| C106104400p | 1.899E+06 | 1.827E+06 | 3.91% | |
| C106154400p | 1.230E+06 | 1.182E+06 | 4.06% | |
| C106204400p | 907.278E+03 | 857.600E+03 | 5.79% |
Trace Resistance results
| Coil Name | Calculated Trace Resistance | Measure Trace Resistance | Error % |
|---|---|---|---|
| C106102200s | 0.981 | 1.2060 | 18.64% |
| C106152200s | 1.472 | 2.1628 | 31.95% |
| C106202200s | 1.962 | 3.4518 | 43.15% |
| C106102400s | 1.598 | 1.7400 | 8.17% |
| C106152400s | 2.397 | 2.9600 | 19.03% |
| C106202400s | 3.196 | 4.7176 | 32.26% |
| C106104200s | 2.894 | 4.9500 | 41.55% |
| C106154200s | 4.340 | 8.9567 | 51.54% |
| C106204200s | 5.787 | 13.9600 | 58.55% |
| C106104400s | 4.712 | 7.1821 | 34.39% |
| C106154400s | 7.068 | 12.6993 | 44.34% |
| C106204400s | 9.424 | 18.3724 | 48.71% |
| C106104200p | 0.723 | 0.9898 | 26.92% |
| C106154200p | 1.085 | 1.7610 | 38.38% |
| C106204200p | 1.447 | 2.8085 | 48.49% |
| C106104400p | 1.178 | 1.4821 | 20.52% |
| C106154400p | 1.767 | 2.7888 | 36.64% |
| C106204400p | 2.356 | 3.7942 | 37.90% |
Source of Error
Parasitic Capacitance
The method I used to approximate the parasitic capacitance is not quite right. As I mentioned above, the coil does have a voltage gradient throughout the coil. However, the most significant potential difference will be in the outer rings for the two-layer board. In 4 layer boards, the voltage potential will alternate between the outer and inner rings as you transition between layers.
A method described in this post[6] could be used to measure both inductance and parasitic capacitance, but ultimately an impedance analyzer would be the best tool for the job.
Trace Resitance
Somewhat surprised by the trace resistance measurement, the measured values were consistently higher than what I predicted. This could be caused by two separate issues that could have a compounding effect.
A. The cumulative error between the voltmeter and current meter could result in a measurement error. If the current meter reads high and the voltmeter reads low, I would be seeing a higher than expected resistance. B. Manufacturing parameters could cause discrepancies if the coil’s dimensions were not the same as the calculated value. If the trace’s height and width were smaller than expected, this would explain a higher resistance.
Conclusion
In the end, I think my approximation seems promising, with consistent alignment between various coil configurations. If I were to do this experiment again, I would have tried to vary the trace width and spacing a bit more to see its effects on parasitic capacitance.
Resonate Frequency
The mathematical approximation used for this experiment proved to provide very accurate results compared to the measured value, in fact, significantly closer than those provided by the TI Coil designer. I can’t explain why these approximations differ so widely without more information about how TI calculates its values. I know that the self inductances are being approximated using the same equation. There was still a discrepancy, which makes me think the main difference is how physical dimensions are calculated.
Parallel Configuation
I don’t think the benefit of wiring the PCI in parallel proved to show much of an advantage. When comparing the similar inductance value from a 2 layer vs 4 layer board, a difference of approximately 1$\Omega$ was seen. I’ll be looking further into this when I start experimenting with how the coils respond to the presence of conductive targets.
Citation
[1]Liu, T., Wei, Z., Chi, H., & Yin, B. (2019). Inductance Calculation of Multilayer Circular Printed Spiral Coils. Journal of Physics: ConferenceSeries, 1176, 062045. doi:10.1088/1742-6596/1176/6/062045
[2]Ulvr, M. (2018). Design of PCB search coils for AC magnetic flux density measurement. AIP Advances, 8(4), 047505. doi:10.1063/1.4991643
[3]Mohan, S.,Hershenson, M., Boyd, S., Lee, T. (1999). Simple Accurate Expressions for Planar Spiral Inductances. IEEE JOURNAL OF SOLID-STATE CIRCUITS, VOL. 34, NO. 10
[4]Oberhauser, .C. (2019). LDC Sensor Design. Texas Instruments White Paper




